

Rotate your ordered pair 90° counter clockwise and turn into a fraction.Ĭongratulations if you made it to the bottom of this post. Going back to our example of 30° or π/6 we get (3,1). Finding Tangent:įollow step one and two for Finding Sine and Cosine: First Quadrant. Step Four:Īpply negative signs where appropriate for the fourth quadrant (the y-value of the order pair). (This is an awkward position for the left handed people)įollow steps one through three for Finding Sine and Cosine: First Quadrant. Fingers will also now represent new positions on the unit circle. Starting from the original position, flip your hand down (reflect over the x-axis). Fingers will also now represent new positions on the unit circle.) Finding Sine and Cosine: Fourth Quadrant This is an awkward position for the right handed people. Or starting from the original position, rotate 180° counter clockwise. (You also have to reflective your hand again, this time over the x-axis. This is exactly the same as Finding Sine and Cosine: Second Quadrant, except for step five, we now negate both value of the ordered pair. Therefore we end up with (-1/2, √3/2) and can conclude that sin(120°) or sin(2π/3) is equal to -1/2 and cos(120°) or cos(2π/3) is equal to √3/2. Since we flipped our hands over the y-axis, we now must switch our values in our ordered pair.įinally we must apply negative signs where appropriate for the second quadrant (the x-value of the order pair). Now we follow steps one through three for Finding Sine and Cosine: First Quadrant.įor example, if we were trying to find the sine/cosine values of 120° or 2π/3 we would get (√3/2, 1/2). It is out of the ordinary and a change of pace from normal math activities. For me I just like it as an activity that the students can remember the lesson by. These students can also very quickly figure it out using the special right triangles or by memorizing the first quadrant. What I have noticed my advanced students love it too because once they have learned this little trick they can quickly use it to recall the piece of the circle they need. With that said this unit circle activity is also good as a last resort for those students who just cannot grasp the creation of the unit circle. So when they hear the terms Unit Circle they think back and go "Oh Yeah! That is the day we did the hand trick." Meaning, something exciting to remember the lesson by and its importance. This activity is meant to create a recall point for your students.
#HOW TO TEACH SPECIAL RIGHT TRIANGLES HOW TO#
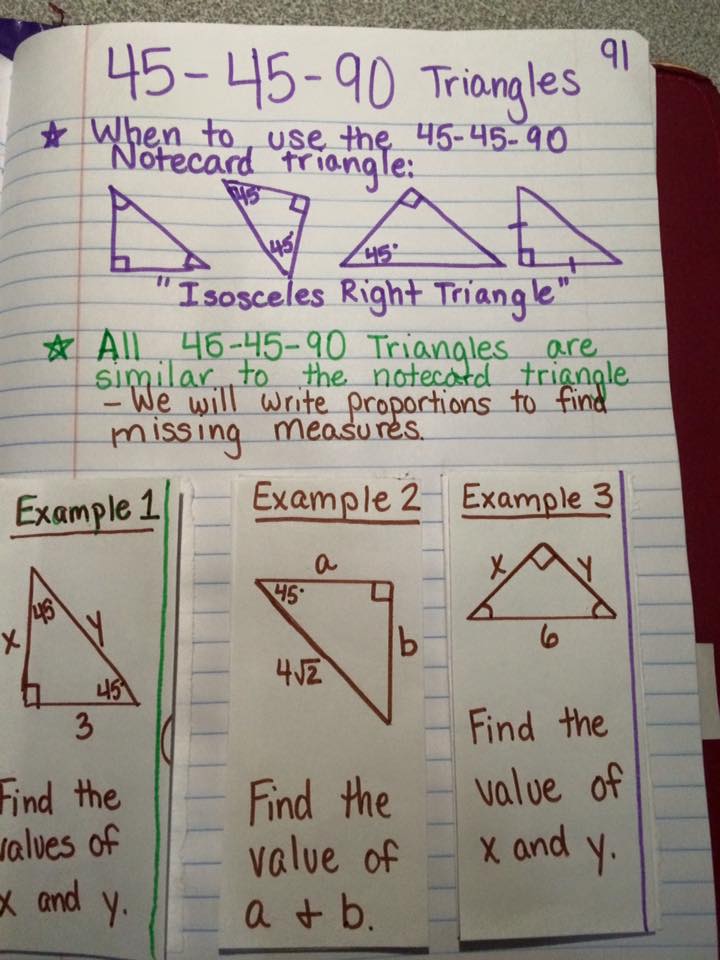
Your students must know how to create it using Special Right Triangles.

IMPORTANT! This activity is a SUPPLEMENT to your lesson on the Unit Circle.


 0 kommentar(er)
0 kommentar(er)
